
- 浅谈电影站是否还有前途?
- 利用Google App Engine免费云空间搭建网站(一)
- 站长必备:从用户访问统计分析挖掘网站的潜在缺陷。
- 田锋林:浅谈B2C网站如何运营
- 我的创业之路(创业十戒)
- 第一曲:了解大淘宝市场以及网店开前心理准备
- 浅谈站长如何才能走得更远
- 新站长如何做淘宝客单品推广
- WP如何不使用插件达到nofollow链接的效果
- 20款优秀免费的Wordpress留言表单插件
- LLsMP系列教程之三:Litespeed开启htaccess伪静态方法
- 吴佛懂:我们需要什么样的电子商务
- 如何挑选适合自己的个性创意域名
- 给新手站长的五条建议
- 商城网站提高网站转化率需从用户角度开始
- 浅析微博营销舍得智慧的应用
- 网站该如何运营才能够走向成功?
- 图示:网站运营过程及内容传播设计
- 站长们,人民币重要还是自己的身体重要?
- 一个大学生做站辛苦网赚成长经历
- 新手站必备的三技术:心态+耐心+坚持
- DNS域名解析服务器出现问题
- SEO工作者总结网站建设的那些事
- 利用谷歌分析工具进行搜索分析(外部搜索篇)
- 查洪江:关键词质量度重要吗?如何提升?
- 我帮新人建网站 累并快乐着
- PR升值很简单
- Drupal入门教程之站点设置篇
- 大漠:如何让你的站群快速被百度收录
- 做好电子商务网站应该注意哪些方面
网络分析与图简介
前面有介绍过使用Gephi来制作传播图,图是Social Network分析最常用的表现形式和方式,这篇文章介绍一下基本的相关知识。点击查看原始文档
Graph的相关基本概念
图(Graph):图是用来表示一组物体之间的关系的方式。
节点(Node):节点是指要分析的物体,每一个物体就是一个节点,比如在Social Network中每个人就是一个节点。
边(Edge):Graph中两个节点间的连线,用于表示两个节点的关系。比如在Social Network中两个人的关注关系,微博传播中转发关系。
度(Degree):节点的度是指与其相连的边数,如果一个节点有3个边,那么这个节点的度就是3。
有向图(Directed Graph):边代表的关系具有方向的图。比如微博的关注关系,就是有方向的。
输入度(In-degree):有向图中一个节点收到的边。
输出度(Out-degree):有向图中一个节点发出的边。
无向图(Undirected Graph):边代表的关系没有方向的图。
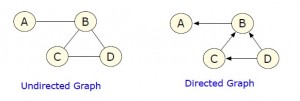
Direct Graph
加权图(Weighted Graph):每个边权重不同的图,边的权重可以代表相似度,距离或者链接成本等。加权图与有向和无向是两个不同的维度。因此,在实际应用中会看到有向加权图(边既有方向又有权重)和无向加权图(边有权重但没有方向)。
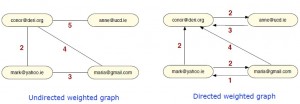
Weighted Graph
属性图(Attributed Graphs):节点和边上可以承载更多的属性,这类图叫做属性图。

Attributed Graph
自我网络(Ego Networks):自我网络关注的不是网络整体而是以个体为中心,通过收集自我焦点关联的节点的信息,可以为个体构建一个局部网络。

Ego Networks
偶图(Bipartite Graphs):在偶图中节点被分成两个独立的集合,以确保同一集合中任意两个节点都不共享一条边。

Actors-Movies Bipartite Graphs
多关系网络(Multi-Relational Networks):在许多社交网络分析(SNA)的应用程序中,在节点间可能存在多种关系。在一种关系网络中节点间距离很近,而在另一种中则可能距离很远。

Multi-Relational Networks
路径(Path):图中从一个节点到另一个节点的一系列的边叫做路径。路径的长度就是边的个数,通常是寻找两个节点间的最短路径。
图的直径:图的直径是指所有节点间的最短路径中的最长的那条。
连通图(Connected Graph):每个节点间都用路径连通的图。反之就是非连通图(Disconnected Graph)。
连通分支(Connected Component):如果一个连通图作为非连通图的一个成分,则这个连通图称为非连通图的连通分支。在许多现实的社交网络中,大部分节点将属于一个巨大的分支。

3 connected components
向心性的计算
临近节点(Neighbourhood):是指与它有边直接相连的节点(不包括它自身)。
集中系数(Clustering Coefficient):节点的集中系数=其临近的节点中有边相连的节点数/其临近节点总数。图的集中系数是其每个节点的聚类系数的平均数。节点的集中系数表现了这个节点的临近节点的集中情况。图的集中系数表明图的集中水平。

Clustering Coefficient
度中心性(Degree Centrality):计算一个节点的边数,度中心性关注单个节点。
Hub节点:度很高的节点。在网络中通常扮演重要的角色。对于一个有向的网络来说,输入度通常用来代表受欢迎程度。

Degree
中介中心性(Betweenness Centrality):出现在许多其他节点间最短路径上的节点有较高的中介中心性分数。

Betweeness Centrality
节点A的度中心性高于节点H,因为节点H的直接连接更少。而节点H有更高的中介中心性,它在这个网络中扮演经纪人的角色,它处在网络内许多节点交往的路径上,因此,它具有控制其他人交往的能力。
特征向量中心性(Eigenvector Centrality):一个节点的特征向量中心性与其临近节点的中心性得分的总和成正比。与重要的节点连接的节点更重要。有少量有影响的联系人的节点其中心性可能超过拥有大量平庸的联系人的节点。这点与PR值类似。
特征向量中心性的计算:
1、计算图的成对临近矩阵的特征分解
2、选择有最大特征值的特征向量
3、第i个节点的中心性等于特征向量中的第i元素
- 上一篇文章: 新手如何利用微博做淘宝客实现月入过万
- 下一篇文章: 巧用Firefox检查代码是否安装正确