八大排序算法 转

概述

排序有内部排序和外部排序，内部排序是数据记录在内存中进行排序，而外部排序是因排序的数据很大，一次不能容纳全部的排序记录，在排序过程中需要访问外存。

我们这里说说八大排序就是内部排序。

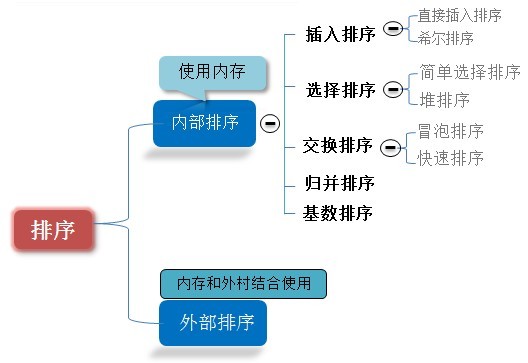
当n较大，则应采用时间复杂度为O(nlog2n)的排序方法：快速排序、堆排序或归并排序序。

快速排序：是目前基于比较的内部排序中被认为是最好的方法，当待排序的关键字是随机分布时，快速排序的平均时间最短；

1.插入排序—直接插入排序(Straight Insertion Sort)

基本思想:

将一个记录插入到已排序好的有序表中，从而得到一个新，记录数增1的有序表。即：先将序列的第1个记录看成是一个有序的子序列，然后从第2个记录逐个进行插入，直至整个序列有序为止。

要点：设立哨兵，作为临时存储和判断数组边界之用。

直接插入排序示例：

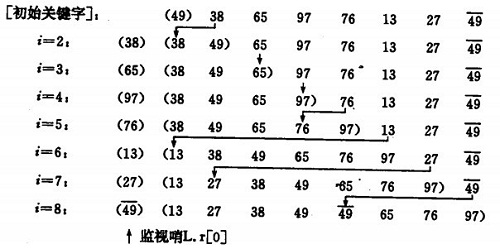
如果碰见一个和插入元素相等的，那么插入元素把想插入的元素放在相等元素的后面。所以，相等元素的前后顺序没有改变，从原无序序列出去的顺序就是排好序后的顺序，所以插入排序是稳定的。

算法的实现：

1. voidPRint(inta[],intn,inti){
2. cout<<i<<":";
3. for(intj=0;j<8;j++){
4. cout<<a[j]<<"";
5. }
6. cout<<endl;
7. }
10. voidInsertSort(inta[],intn)
11. {
12. for(inti=1;i<n;i++){
13. if(a[i]<a[i-1]){//若第i个元素大于i-1元素，直接插入。小于的话，移动有序表后插入
14. intj=i-1;
15. intx=a[i];//复制为哨兵，即存储待排序元素
16. a[i]=a[i-1];//先后移一个元素
17. while(x<a[j]){//查找在有序表的插入位置
18. a[j+1]=a[j];
19. j--;//元素后移
20. }
21. a[j+1]=x;//插入到正确位置
22. }
23. print(a,n,i);//打印每趟排序的结果
24. }
26. }
28. intmain(){
29. inta[8]={3,1,5,7,2,4,9,6};
30. InsertSort(a,8);
31. print(a,8,8);
32. }

效率：

时间复杂度：O（n^2）.

其他的插入排序有二分插入排序，2-路插入排序。

2. 插入排序—希尔排序（Shell`s Sort）

希尔排序是1959 年由D.L.Shell 提出来的，相对直接排序有较大的改进。希尔排序又叫缩小增量排序

基本思想：

先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序，待整个序列中的记录“基本有序”时，再对全体记录进行依次直接插入排序。

操作方法：

1. 选择一个增量序列t1，t2，…，tk，其中ti>tj，tk=1；
2. 按增量序列个数k，对序列进行k 趟排序；
3. 每趟排序，根据对应的增量ti，将待排序列分割成若干长度为m 的子序列，分别对各子表进行直接插入排序。仅增量因子为1 时，整个序列作为一个表来处理，表长度即为整个序列的长度。

希尔排序的示例：

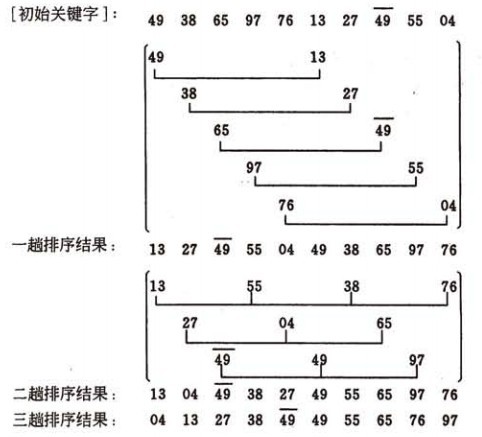
算法实现：

我们简单处理增量序列：增量序列d = {n/2 ,n/4, n/8 .....1}n为要排序数的个数

即：先将要排序的一组记录按某个增量d（n/2,n为要排序数的个数）分成若干组子序列，每组中记录的下标相差d.对每组中全部元素进行直接插入排序，然后再用一个较小的增量（d/2）对它进行分组，在每组中再进行直接插入排序。继续不断缩小增量直至为1，最后使用直接插入排序完成排序。

1. voidprint(inta[],intn,inti){
2. cout<<i<<":";
3. for(intj=0;j<8;j++){
4. cout<<a[j]<<"";
5. }
6. cout<<endl;
7. }
8. /**
9. *直接插入排序的一般形式
10. *
11. *@paramintdk缩小增量，如果是直接插入排序，dk=1
12. *
13. */
15. voidShellInsertSort(inta[],intn,intdk)
16. {
17. for(inti=dk;i<n;++i){
18. if(a[i]<a[i-dk]){//若第i个元素大于i-1元素，直接插入。小于的话，移动有序表后插入
19. intj=i-dk;
20. intx=a[i];//复制为哨兵，即存储待排序元素
21. a[i]=a[i-dk];//首先后移一个元素
22. while(x<a[j]){//查找在有序表的插入位置
23. a[j+dk]=a[j];
24. j-=dk;//元素后移
25. }
26. a[j+dk]=x;//插入到正确位置
27. }
28. print(a,n,i);
29. }
31. }
33. /**
34. *先按增量d（n/2,n为要排序数的个数进行希尔排序
35. *
36. */
37. voidshellSort(inta[],intn){
39. intdk=n/2;
40. while(dk>=1){
41. ShellInsertSort(a,n,dk);
42. dk=dk/2;
43. }
44. }
45. intmain(){
46. inta[8]={3,1,5,7,2,4,9,6};
47. //ShellInsertSort(a,8,1);//直接插入排序
48. shellSort(a,8);//希尔插入排序
49. print(a,8,8);
50. }

3. 选择排序—简单选择排序（Simple Selection Sort）

基本思想：

在要排序的一组数中，选出最小（或者最大）的一个数与第1个位置的数交换；然后在剩下的数当中再找最小（或者最大）的与第2个位置的数交换，依次类推，直到第n-1个元素（倒数第二个数）和第n个元素（最后一个数）比较为止。

简单选择排序的示例：

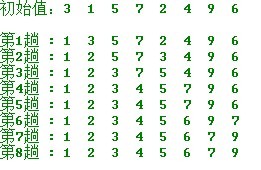
操作方法：

第一趟，从n 个记录中找出关键码最小的记录与第一个记录交换；

第二趟，从第二个记录开始的n-1 个记录中再选出关键码最小的记录与第二个记录交换；

以此类推.....

第i 趟，则从第i 个记录开始的n-i+1 个记录中选出关键码最小的记录与第i 个记录交换，

直到整个序列按关键码有序。

算法实现：

1. voidprint(inta[],intn,inti){
2. cout<<"第"<<i+1<<"趟:";
3. for(intj=0;j<8;j++){
4. cout<<a[j]<<"";
5. }
6. cout<<endl;
7. }
8. /**
9. *数组的最小值
10. *
11. *@returnint数组的键值
12. */
13. intSelectMinKey(inta[],intn,inti)
14. {
15. intk=i;
16. for(intj=i+1;j<n;++j){
17. if(a[k]>a[j])k=j;
18. }
19. returnk;
20. }
22. /**
23. *选择排序
24. *
25. */
26. voidselectSort(inta[],intn){
27. intkey,tmp;
28. for(inti=0;i<n;++i){
29. key=SelectMinKey(a,n,i);//选择最小的元素
30. if(key!=i){
31. tmp=a[i];a[i]=a[key];a[key]=tmp;//最小元素与第i位置元素互换
32. }
33. print(a,n,i);
34. }
35. }
36. intmain(){
37. inta[8]={3,1,5,7,2,4,9,6};
38. cout<<"初始值：";
39. for(intj=0;j<8;j++){
40. cout<<a[j]<<"";
41. }
42. cout<<endl<<endl;
43. selectSort(a,8);
44. print(a,8,8);
45. }

简单选择排序的改进——二元选择排序

简单选择排序，每趟循环只能确定一个元素排序后的定位。我们可以考虑改进为每趟循环确定两个元素（当前趟最大和最小记录）的位置,从而减少排序所需的循环次数。改进后对n个数据进行排序，最多只需进行[n/2]趟循环即可。具体实现如下：

1. voidSelectSort(intr[],intn){
2. inti,j,min,max,tmp;
3. for(i=1;i<=n/2;i++){
4. //做不超过n/2趟选择排序
5. min=i;max=i;//分别记录最大和最小关键字记录位置
6. for(j=i+1;j<=n-i;j++){
7. if(r[j]>r[max]){
8. max=j;continue;
9. }
10. if(r[j]<r[min]){
11. min=j;
12. }
13. }
14. //该交换操作还可分情况讨论以提高效率
15. tmp=r[i-1];r[i-1]=r[min];r[min]=tmp;
16. tmp=r[n-i];r[n-i]=r[max];r[max]=tmp;
18. }
19. }

4. 选择排序—堆排序（Heap Sort）

堆排序是一种树形选择排序，是对直接选择排序的有效改进。

基本思想：

堆的定义如下：具有n个元素的序列（k1,k2,...,kn),当且仅当满足

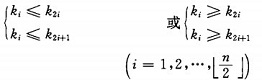
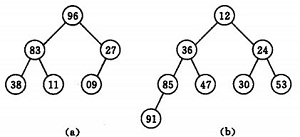
时称之为堆。由堆的定义可以看出，堆顶元素（即第一个元素）必为最小项（小顶堆）。若以一维数组存储一个堆，则堆对应一棵完全二叉树，且所有非叶结点的值均不大于(或不小于)其子女的值，根结点（堆顶元素）的值是最小(或最大)的。如：

（a）大顶堆序列：（96, 83,27,38,11,09)

(b) 小顶堆序列：（12，36，24，85，47，30，53，91）

初始时把要排序的n个数的序列看作是一棵顺序存储的二叉树（一维数组存储二叉树），调整它们的存储序，使之成为一个堆，将堆顶元素输出，得到n 个元素中最小(或最大)的元素，这时堆的根节点的数最小（或者最大）。然后对前面(n-1)个元素重新调整使之成为堆，输出堆顶元素，得到n 个元素中次小(或次大)的元素。依此类推，直到只有两个节点的堆，并对它们作交换，最后得到有n个节点的有序序列。称这个过程为堆排序。

因此，实现堆排序需解决两个问题：1. 如何将n 个待排序的数建成堆；2. 输出堆顶元素后，怎样调整剩余n-1 个元素，使其成为一个新堆。

首先讨论第二个问题：输出堆顶元素后，对剩余n-1元素重新建成堆的调整过程。调整小顶堆的方法：

1）设有m 个元素的堆，输出堆顶元素后，剩下m-1 个元素。将堆底元素送入堆顶（（最后一个元素与堆顶进行交换）